今回は、大学化学で登場するファントホッフの式を紹介します。
ファントホッフの式とは
ファントホッフの式とは、平衡定数の自然対数を温度の関数としてプロットしたときの勾配を表す式です。
ファントホッフの式
ファントホッフの式は、以下の式で表されます。
\[\frac{dlnK}{dT}=\frac{\Delta_rH^\circ}{RT^2}\]
また、次式で表されることもあります。
\[\frac{dlnK}{d\left(\frac{1}{T}\right)}=-\frac{\Delta_rH^\circ}{R}\]
ファントホッフの式の導出
熱力学的平衡定数Kは以下の式で表される。
\[\Delta_rG^\circ=-RTlnK\]
式を変形すると、
\[lnK=-\frac{\Delta_rG^\circ}{RT}\]
となり、これを\(lnK\)で微分すると、
\[\frac{dlnK}{dT}=-\frac{1}{R}\frac{d\left(\frac{\Delta_rG^\circ}{T}\right)}{dT}\]
となる。ここで、\(K\)と\(\Delta_rG^\circ\)は温度のみに依存するので、微分は完全微分である。
ギブズーヘルムホルツの式\(d(\Delta/T)/dT=-\Delta H/T^2\)を、
\[\frac{d\left(\frac{\Delta_rG^\circ}{T}\right)}{dT}=-\frac{\Delta_rH^\circ}{T^2}\]
のかたちで利用する。ここで、\(\Delta_rH^\circ\)は温度\(T\)における標準反応エンタルピーである。
この2式を組み合わせると、ファントホッフの式が得られる。
変化形の方は、
\[\frac{d\left(\frac{1}{T}\right)}{dT}=\frac{1}{T^2}\]
つまり
\[dT=-T^2d\left(\frac{1}{T}\right)\]
を用いれば導ける。ファントホッフの式の原形にこれを代入すると、
\[-\frac{dlnK}{T^2d\left(\frac{1}{T}\right)}=\frac{\Delta_rH^\circ}{RT^2}\]
となり、これを整理すれば変化形となる。
ファントホッフの式を用いた例題
問題
反応\(2SO_2(g)+O_2(g)\to2SO_3(g)\)の平衡定数は、300Kで\(4.0\times10^{24}\)、500Kで\(2.5\times10^{10}\)、700Kで\(3.0\times10^{4}\)である。500Kにおける反応エンタルピーを見積もりなさい。(都合により、反応式の矢印は誤った表現となっている)
解法
ファントホッフの式(変化形)からわかるように、反応エンタルピーは温度に依存しないと仮定してもよいので、\(1/T\)を横軸にとり、\(-lnK\)をプロットすると勾配が\(\Delta_rH^\circ/R\)の直線になるはずである。
解答
\[\begin{array}{c|ccc}T/K&300&500&700\\(10^3K)/T&3.33&2.00&1.43\\-lnK&-56.6&-23.9&-10.3\end{array}\]
これらの点を下図のようにプロットする。
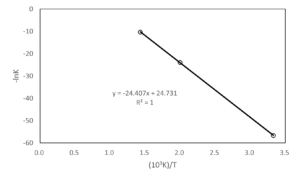
グラフの勾配は\(-24.4\times10^3K\)であるので、
\[\Delta_rH^\circ=(-24.4\times10^3K)\times R=-202kJ mol^{-1}\]
が得られる。