【グラフ攻略】Excel(エクセル)の近似曲線をマスターしよう！【初心者向け】

Excel（エクセル）は、データ解析やグラフ作成のための多目的なツールとして広く利用されています。その中でも、Excelの近似曲線機能は、データの傾向やパターンを視覚化するのに役立ちます。この記事では、Excelの近似曲線について解説します。

近似曲線とは？

近似曲線は、実際のデータ点を通過するように引かれる理論的な曲線です。これにより、データの傾向やパターンを把握しやすくなります。Excelの近似曲線機能は、データの散布図に対して、最適な近似曲線を自動的に計算して表示します。

Excelでの近似曲線の作成方法

Excelで近似曲線を作成する手順は次の通りです。

近似曲線の解釈

近似曲線は、データの傾向やパターンを示すだけでなく、将来の値の予測やトレンドの確認にも役立ちます。また、Excelは近似曲線の精度を示すR²値（決定係数）を表示するため、近似曲線の適合度を評価するのに役立ちます。R²値が1に近いほど、データが曲線によく適合していることを意味します。

注意点と応用例

• 近似曲線は、データの傾向を示す手段であるため、必ずしもすべてのデータ点と完全に一致するわけではありません。
• 近似曲線を使用して将来の値を予測する場合、データの範囲外での精度は低くなる可能性があります。

Excelの近似曲線機能は、さまざまな分野で広く活用されています。例えば、販売データの分析、株価の予測、科学実験の結果の解釈など、さまざまな応用が考えられます。

Excel(エクセル)で使える近似曲線

エクセルでは、以下の6種類の近似曲線があります。

これらの中には似ているものもありますが、それぞれ少しずつ異なる役割を持っています。

そのため、データを処理する場面では、適切な近似曲線を選ぶことが求められます。

適切な近似曲線を選ぶことができるように、簡単な知識は覚えておくようにしましょう。

では、ひとつずつ解説していきます。

指数近似

指数近似は、数学的なモデルを用いてデータを近似する手法の一つです。指数関数は以下の形式で表されます。

\[y = a \cdot e^{bx}\]

ここで、\(y\) は目的変数（従属変数）、\(x\) は説明変数（独立変数）、\(a\) は定数、\(b\) は指数関数の傾き（指数部の係数）を表します。指数近似は、この指数関数を用いてデータをモデル化し、実際の観測値に最も適合するパラメータ \(a\) と \(b\) を求めることで行われます。

指数近似は、特にデータが急速に増加または減少する場合に有用です。例えば、バクテリアの増殖、化学反応の速度、経済成長などの現象をモデル化する際によく使用されます。指数関数は指数部が増減することで急激な変化を表現するため、これらの現象に適しています。

指数近似を行う際には、まずデータを対数変換して線形関係を作り、最小二乗法などの手法を用いてパラメータ \(a\) と \(b\) を推定します。その後、元のデータに戻すことで指数近似曲線を得ることができます。

指数近似の利点は、データの急速な増減をモデル化することができること、また、相対的に単純な形式であるため、解釈が容易であることです。一方で、指数関数が無限大に発散することがあるため、データの範囲外での予測精度が低下する可能性があります。また、指数近似を行う場合は、データの特性や背景をよく理解し、適切なモデルを選択することが重要です。

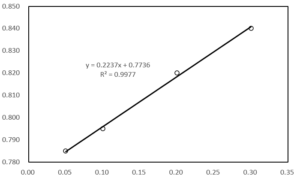
線形近似

線形近似は、数学的なモデルを用いてデータを近似する手法の一つです。線形近似では、データを線形関数（直線）で近似することを目指します。一般的に、線形関数は以下の形式で表されます。

\[y = mx + c\]

ここで、\(y\) は目的変数（従属変数）、\(x\) は説明変数（独立変数）、\(m\) は直線の傾き（係数）、\(c\) は直線の切片を表します。線形近似は、この直線モデルを用いて実際のデータに最も適合する \(m\) と \(c\) を求めることで行われます。

線形近似は、データの傾向やパターンを捉える上で非常に有用です。直線は単純な形式であり、直感的に理解しやすいため、解釈が容易です。また、線形近似は、データが直線的な傾向を持つ場合に特に適しています。例えば、時間と温度の関係や、変数間の比例関係などの現象をモデル化する際によく使用されます。

線形近似を行う際には、最小二乗法などの手法を用いて、実際のデータと近似直線との残差（誤差）を最小化する \(m\) と \(c\) を求めます。最小二乗法は、観測されたデータ点と近似直線の距離の二乗和を最小化することで、最適なパラメータを求める手法です。

線形近似の利点は、直線が単純であるため、解釈が容易であり、また、データの傾向を比較的正確に捉えることができることです。一方で、データが非線形な関係を持つ場合には適用できないことがあります。また、線形近似は、近似直線がデータに完全に一致するわけではないため、近似の精度を適切に評価する必要があります。

対数近似

対数近似は、データの傾向を対数変換を用いて近似する手法です。対数近似では、データを対数スケールでプロットし、直線的な関係を持つ場合に近似直線を求めます。対数近似は、特にデータが指数的に増加または減少する場合に有用です。

対数近似は、対数関数を用いてデータを近似することを目指します。一般的に、対数関数は以下の形式で表されます。

\[y = a \cdot \log x + b\]

ここで、\(y\) は目的変数（従属変数）、\(x\) は説明変数（独立変数）、\(a\) と \(b\) は定数を表します。対数近似では、対数変換を行ったデータに対して、線形近似を行います。つまり、対数変換後のデータを線形関係としてモデル化し、最小二乗法などの手法を用いて近似直線の傾き \(a\) と切片 \(b\) を求めます。

対数近似は、特にデータが指数関数的な傾向を持つ場合に有用です。例えば、バクテリアの増殖、化学反応の速度、経済成長などの現象をモデル化する際によく使用されます。対数変換によって、指数関数的なデータを線形的に近似することができ、直線の傾きや切片からデータの傾向を推定することが可能になります。

対数近似の利点は、対数変換によってデータの変動幅が縮小し、データのばらつきが小さくなるため、直線的な関係を捉えやすくなることです。また、対数関数は比較的単純な形式であり、解釈が容易です。一方で、対数近似は対数変換が必要となるため、データの背景や特性を考慮して適切な手法を選択する必要があります。

下のグラフは、片対数グラフです。

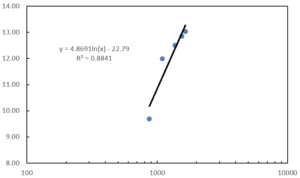
このように、対数近似を使えば、片対数グラフで直線を引くことができます。

多項式近似

多項式近似は、データを多項式関数で近似する手法です。多項式関数は以下の形式で表されます。

\[y = a_{n}x^{n} + a_{n-1}x^{n-1} + \cdots + a_{1}x + a_{0}\]

ここで、\(y\) は目的変数（従属変数）、\(x\) は説明変数（独立変数）、\( a_n ,a_{n−1}, \ldots , a_1, a_0 \) は係数を表します。\(n\) は多項式の次数を示し、多項式近似の精度を決定します。

多項式近似では、与えられたデータに最も適合する多項式関数を求めます。一般的に、次数 \(n\) の多項式は \( (n+1) \) 個の係数を持ちます。そのため、与えられたデータに対して最もよく適合する多項式を見つけるには、最小二乗法などの手法を用いて、係数を調整します。

多項式近似は、データの非線形な関係をモデル化するために使用されます。直線や指数関数ではデータをうまく近似できない場合に有用です。例えば、物理学や工学での実験データ、金融データの解析、気象データの予測などの分野でよく利用されます。

多項式近似の利点は、多項式関数が非常に柔軟であり、様々な形状のデータに適用できることです。また、多項式関数は比較的簡単な形式であるため、解釈が容易です。一方で、高次の多項式を使用すると過学習のリスクが高まり、未知のデータに対する予測精度が低下する可能性があります。そのため、適切な次数の多項式を選択し、モデルの複雑さを調整することが重要です。

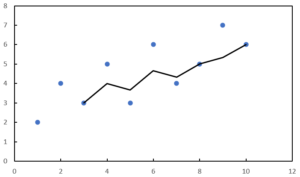
多項式近似を用いると、下のようなグラフが得られます。

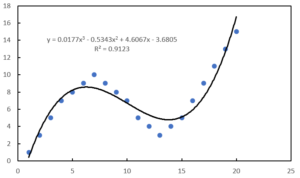
増減の回数によって、次数を決定します。

たとえば、上のグラフのように「増える・減る・増える」の場合の次数は”3″です。

「増える・減る・増える・減る」の場合は、”4″になります。

累乗近似

累乗近似は、データを累乗関数で近似する手法です。累乗関数は以下の形式で表されます。

\[y = a \cdot x^{b}\]

ここで、\(y\) は目的変数（従属変数）、\(x\) は説明変数（独立変数）、\(a\) と \(b\) は定数を表します。\(a\) は定数項で、\(b\) は累乗の指数を示します。

累乗近似では、与えられたデータに最も適合する累乗関数を求めます。一般的に、累乗関数の形式は対数変換を施すことで線形関係に変換されます。対数変換を行うと、累乗関数が次のような線形関係として表現されます。

\[\log y = \log a + b \log x\]

この線形関係に対して最小二乗法などの手法を用いて、\( \log a \) と \(b\) を求めます。そして、\(a\) と \(b\) を求めることで累乗近似のパラメータを得ることができます。

累乗近似は、データが指数的に増加または減少する場合に有用です。例えば、物理学や工学での実験データ、生物学での成長曲線の解析、経済学での成長モデルの構築などの分野でよく利用されます。また、累乗関数はしばしばべき乗則（power law）として知られており、自然界や社会現象など様々な現象に見られるパターンをモデル化するために用いられます。

累乗近似の利点は、データが指数的な関係を持つ場合に非常に適していることです。また、累乗関数は比較的単純な形式であり、解釈が容易です。一方で、データが指数関数的な関係を持たない場合には不適切であり、過度のフィッティング（過剰適合）に注意する必要があります。

下のグラフは、両対数グラフです。

 

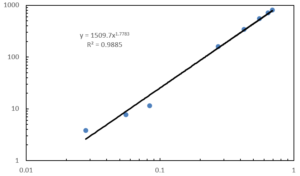
両対数グラフで線形近似などを使ってしまうと、曲線になってしまいます。

それに対し、累乗近似を使えば、直線を引くことができます。

これは、両対数グラフの特性と累乗近似を理解していれば、当然のことだと感じるでしょう。

移動平均

移動平均（Moving Average）は、データの変動を平滑化し、トレンドや周期性を把握するための統計的手法です。時間の経過に伴うデータの変動を把握する際に特に有用です。移動平均は、一定期間のデータの平均を取り、その平均値を新たなデータ点として出力することで行われます。

一般的に、移動平均は次の手順で計算されます。

1. 一定期間のデータ（例えば、日次、週次、月次など）を選択します。
2. 選択した期間内のデータの平均を計算します。
3. 平均を新たなデータ点として出力します。
4. 次の期間に移動し、同様の手順を繰り返します。

移動平均の期間を長くすると、データの変動がより滑らかになりますが、過去の情報に反応する速度が遅くなります。一方、期間を短くすると、データの変動に対する反応速度は速くなりますが、ノイズやランダムな変動がより強調される傾向があります。

移動平均は、主に次のような目的で使用されます。

• トレンドの確認：長期的なトレンドを把握するために使用されます。特に季節性の影響を除去し、トレンドを明確にする場合に有用です。
• データの平滑化：ノイズやランダムな変動を除去して、データの本質的な傾向を把握するために使用されます。
• 予測の改善：過去のデータのパターンを基に、将来の値を予測する際に使用されます。

移動平均は、経済学、ファイナンス、気象学、医学、品質管理などのさまざまな分野で広く使用されています。一般的なタイプの移動平均には、単純移動平均（Simple Moving Average）、加重移動平均（Weighted Moving Average）、指数平滑化移動平均（Exponential Moving Average）などがあります。それぞれの方法は、データの特性や用途に応じて選択されます。

このような値が測定されたとします。

このとき、区間を3に設定していれば、\(x=3\) のときの \(y\) は、\(\frac{(2+4+3)}{3}=3\)となります。

グラフを作成すると、以下のようになります。

近似曲線の選び方

ここまで簡単に各近似曲線の解説をしました。

概要は理解できたと思いますが、細かい部分がまだ微妙だと思います。

そこで、迷った時の選び方を紹介します。

解析するデータの種類

データの種類によって、出てくる式の検討がつくときもあると思います。

その場合は、その式になるように近似曲線を選んでください。

logやe(ネイピア数)などを使えるか

理系の方でしたら、\( \log \) や \(e\) は身近なものです。

しかし、それ以外の人には嫌厭されるかもしれません。

そのような人を対象にデータを説明するときは、できるだけ難しい計算記号の使用を避けましょう。

わかりやすい数式になっているか

数式を見て、パッと理解できることも大切です。

見た目の美しさまで気を配れたら、よりよいグラフに仕上がります。

R²値はいくつか

最後の決め手となるのが、R²値です。

一般的に、R²値が1に近い方が正確な近似曲線になっています。

なので、判断ができないときは、R²値が1に近い方を選びましょう。

まとめ

以下の表を使って考えると、わかりやすいです。

線形近似	一般的なグラフ
指数近似	片対数グラフ（縦軸が対数）
対数近似	片対数グラフ（横軸が対数）
累乗近似	両対数グラフ
多項式近似	値が「増加・減少」を繰り返す

 最後に